楽音(がくおん)・噪音(そうおん)・基準音(440Hz)・12平均律・オクターブ (テキストと画像での解説)
※ テキストと画像での解説内容は、動画での解説内容と同じものとなっています。
音楽で使われる音には、ピアノやギター、管楽器のように、
「音波の周期」(つまり周波数の事) がある程度一定で、
明確に音の高さを認識できる「楽音」(がくおん) と、
ドラムなどの楽器のように、音の高さが明確ではない「噪音」(そうおん) があります。
基準音(440Hz) と 12平均律とは
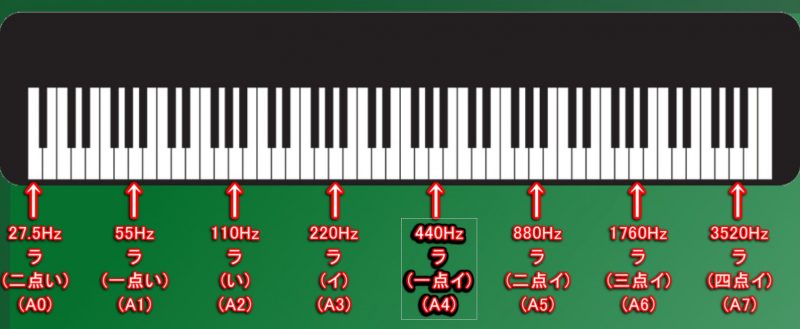
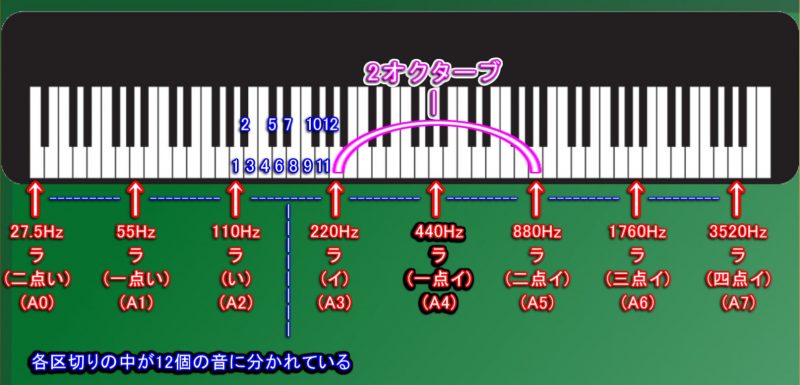
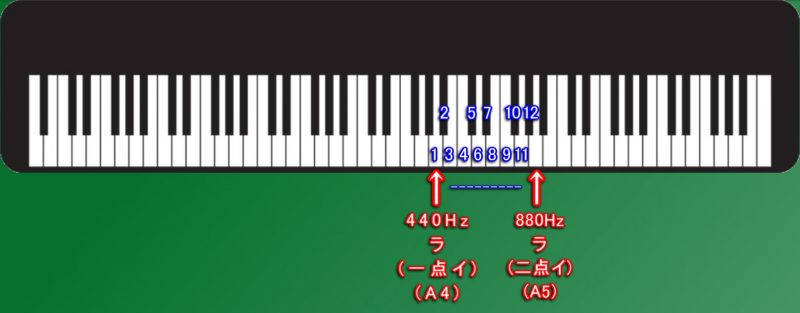
ピアノやギターなどの楽器で鳴らされる「楽音」では、「440Hz」の音を基準として、
「440Hz」の「1/2の周波数」( 220Hz ・ 110Hz ・55Hz ・ 27.5Hz ) と、
「2倍の周波数」(880Hz ・ 1760Hz ・ 3520Hz )ごとに区切り、
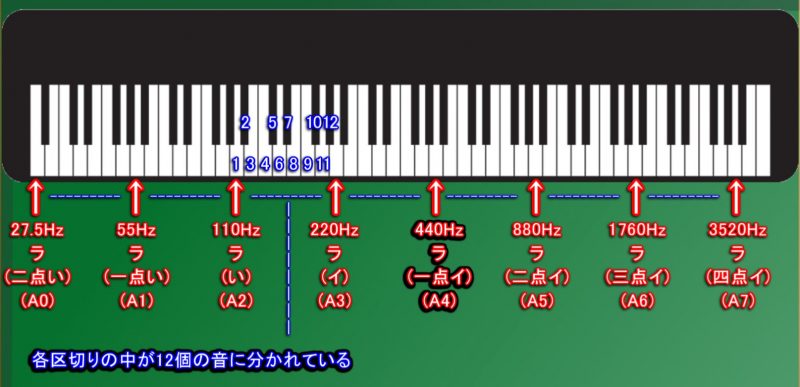
区切った各周波数の範囲の中を12分割した高さの音が「楽音」として使われます。
このように、基準音から「2倍」・「1/2」に区切った範囲を12分割する「調律法」(楽音の周波数の調整方法) の事を「12平均律」(じゅうにへいきんりつ) と言います。
※ ただ、最近では、「基準音」を「442Hz」などにして、
「442Hz」の「1/2の周波数」( 221Hz ・ 110.5Hz ・55.25Hz ・ 27.75Hz ) 、
「2倍の周波数」(884Hz ・ 1768Hz ・ 3536Hz )ごとに区切り、
区切った各周波数の範囲の中を12分割した高さの音を「楽音」として使ったりもします。
オクターブとは
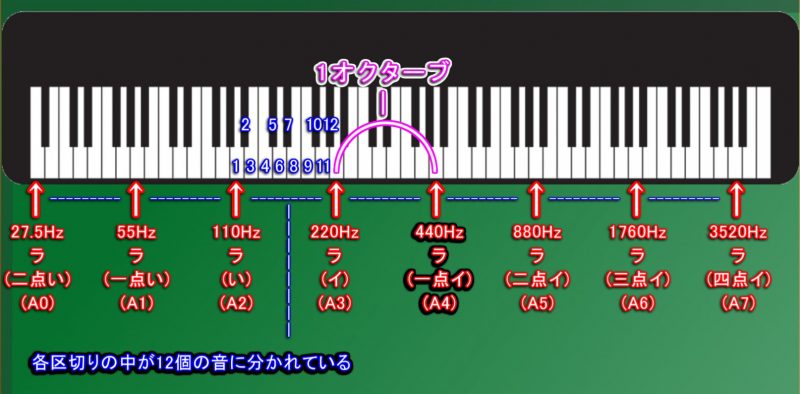
また、ある高さの音から 「1/2の周波数」にした音の範囲、
または、「2倍の周波数」にした音の範囲の事を「オクターブ」と言います。
※ 「オクターブ」というのは、必ずしも「440Hz」( ラ / A4) を基準として「1/2」・「2倍」にした周波数の範囲の事だけを言うのではなく、
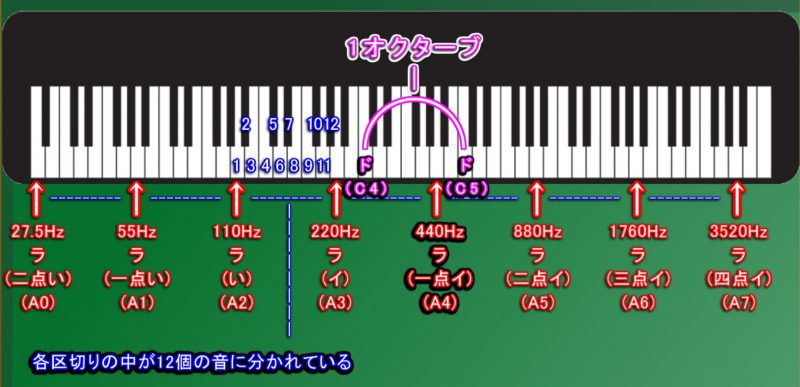
「ド」(C4 / 一点ハ) から 「ド」(C5 / 二点ハ)までの範囲においても、周波数が「1/2」・「2倍」になっているので、「オクターブ」と呼びます。
また、「オクターブ」の範囲が1つだけの場合、「1オクターブ」(いちオクターブ)、
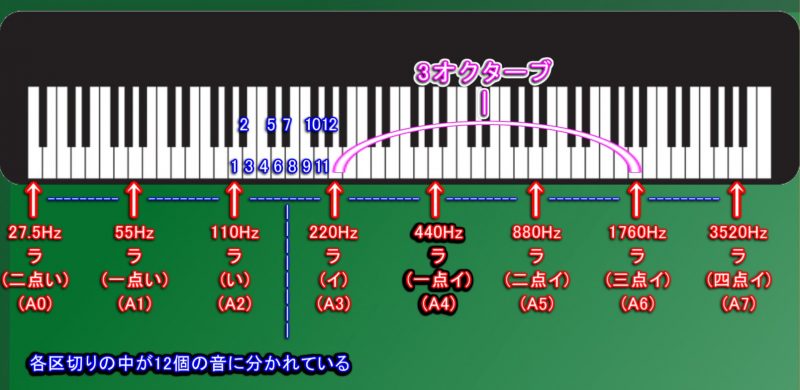
「オクターブ」の範囲が2つなら「2オクターブ」(にオクターブ)と言います。
同じように、「3オクターブ」・「4オクターブ」、といった感じで、音の範囲を言う際、
「オクターブ」に「1、2、3、、、」と付けて言います。
※ 例えば、
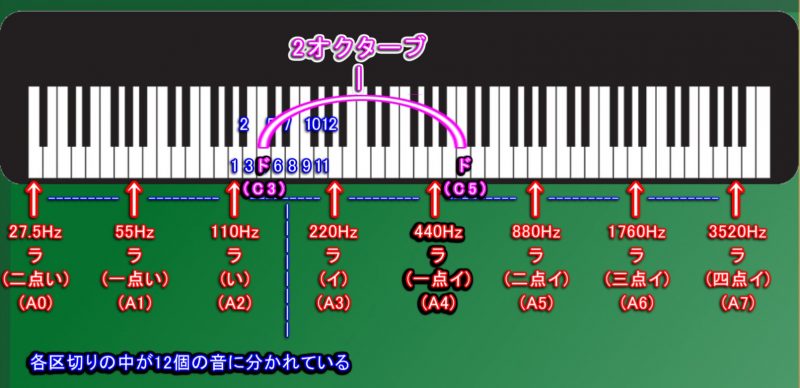
「C3」(ド / ハ / 約130.81Hz) の音から
「C5」(ド / 二点ハ / 約523.25Hz)
の音の範囲で声が出せる場合、
”2オクターブの声域(声で出せる音域)” と言います。
※ 他にも、”1オクターブ上の音でメロディーを歌う事って出来る?” といった感じで
「オクターブ」という言葉は使われたります。
それでは、以上で、”楽音(がくおん)・噪音(そうおん)・基準音(440Hz)・12平均律・オクターブ”
についての解説は終了となりますが、
最後に、「12平均律」と「純正律」についての雑学を少しかいつまんで解説します。
12平均律と純正律について
元々、音楽で使われる「楽音」には、「純正律」(じゅんせいりつ) という調律法が使われていました。
少し話が変わりますが、違う高さの音が同時に2つ以上鳴った状態を「和音」(コード)と言います。
2つの音(または2つ以上の音) が綺麗に響き合う理由は、2つの音(または2つ以上の音) の周波数の比率が整っているからです。
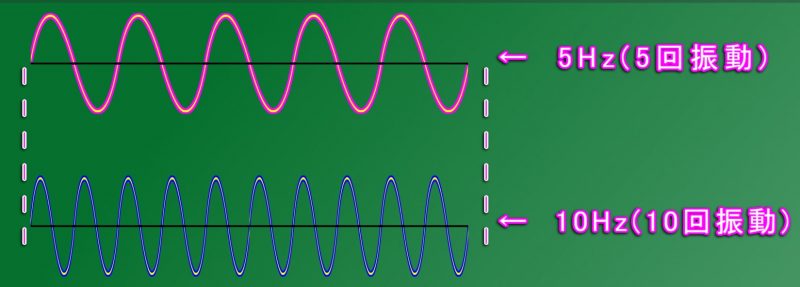
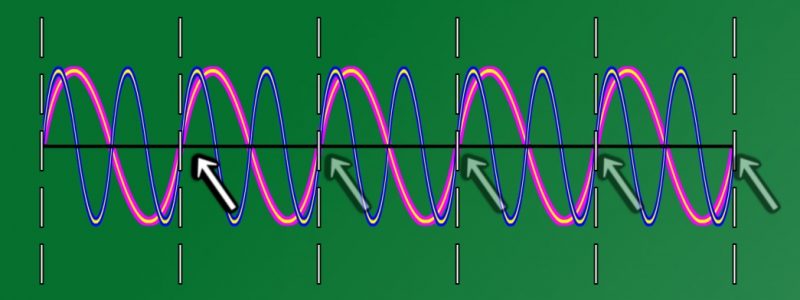
例えば、「5Hz」と「10Hz」では、周波数の比率が、「5Hz」から見ると「2倍」、
「10Hz」からみると「1/2」、というように整数倍の整った比率なので、
「5Hz」の音と「10Hz」の音を重ね合わせると、
「5Hz」の音 (ピンク) の2回目の振動が始まる箇所で、
「10Hz」の音 (青色) の3回目の振動が始まる箇所が重なるようになっています。
このように、2つの音の周波数の比率が整っていると、
振動の周期が どこかで重なり合うので、
綺麗に響きあって聴こえる、という訳です。
今回は、整数倍の「5Hz」と「10Hz」を例に挙げましたが、
「10Hz」と「15Hz」のように、「1.5倍」などの
整った小数倍の周波数比率でも綺麗に響き合います。
かなり大雑把な説明になりますが、
「純正律」という調律方法では、
周波数の比率が綺麗に整うように調律します。
ただ、周波数の比率が綺麗に整うように調律するため、
1オクターブ内が7音だけで作られていた時代もあり、
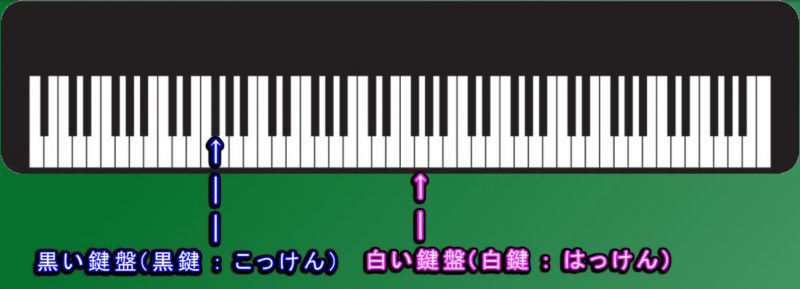
その時代ではピアノの鍵盤には、黒い鍵盤(黒鍵 : こっけん) は無く、
白い鍵盤(白鍵 : はっけん) だけでした。
しかし、使える楽音が少ないと、限られた表現の曲になってしまいますし、
「キー」(調) や 「スケール」(音階) も限られてしまったりなど、様々な経緯があり、「12平均律」が使われるようになったようです。
「12平均律」であれば、使える楽音の数が増えるので、表現の幅が広がりますし、
どの楽音からでも「メジャーキー」(長調)・「マイナーキー」(短調) が作れて、
「スケール」(音階) も、様々なスケールが使えるようになります。
ただ、「純正律」とは違い、「12平均律」では1オクターブを12分割しているため、
各楽音の周波数が小数点第3位になっていたりするので、
「純正律」と比べて周波数が整っていません。
そのため、「12平均律」での「コード」(和音)の響きは、「純正律」での「コード」(和音)より綺麗な響きにはなりません。
ちなみに、「12平均律」という名称ではありますが、
各オクターブ間の周波数を「12」で割ったとしても割り切れないので均等にはなりませんし、
均等に周波数を上げているわけではなく、周波数比率が均等に上がっていっている訳でもありません。
※ 例えば、「440Hz」から「880Hz」までの周波数は「440Hz」(880 – 440 = 440)ですから、
「440Hz」を「12」で分割する事になるのですが、「440 ÷ 12 = 36.666….」というように割り切れません。
この「12平均律」や「純正律」などの調律の話を、正確に理解しようとすると、周波数の比率や、音楽の歴史、調律法など、様々な知識が必要になりますし、ポップスやロックなどの音楽ジャンルや、DTMを行う際には、そこまでの知識が無くても作曲などが出来るので、細かくは割愛させて頂きます( > < )

ただ、「純正律」や「12平均律」などの調律法についての話は、
ググると様々なサイトやブログで説明されていて、
何世紀も前の音楽家たちが研究を重ねて作り上げていたり、
今なお、音楽家の間でも議論されていて、
単純に話として面白いので、
興味がある人は「純正律 平均律」などのキーワードで
ググってみて頂ければと思います ( ^ ^ )